我们正在研究生物的进化历程。除了最初的生物外,所有生物都由已存在的生物进化而来。我们把已存在的生物称为父母生物,新诞生的生物称为子生物。
$N$ 个生物各有一个独一无二的出生编号,范围从 $0$ 到 $N-1$。这些编号按生物诞生的顺序分配,因此父母生物的出生编号总是小于子生物的编号,而最初生物的出生编号为 $0$。
生物通过进化诞生的过程可以用一个树形结构来表示:生物是树中的节点,进化关系是连接父母生物和子生物的边,最初生物作为树的根。这个结构被称为进化树。
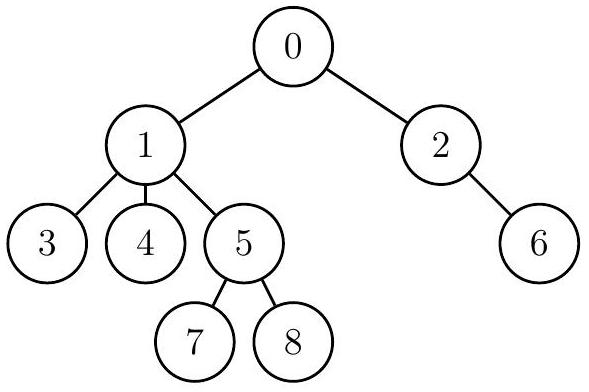
例如,假设最初编号为 $0$ 的生物进化出编号为 $1$ 和 $2$ 的生物,编号 $1$ 的生物进化出编号 $3$、$4$、$5$ 的生物,编号 $2$ 的生物进化出编号 $6$ 的生物,而编号 $5$ 的生物又进化出编号 $7$ 和 $8$ 的生物,这样的进化树如下图所示,每个节点标有生物的出生编号。
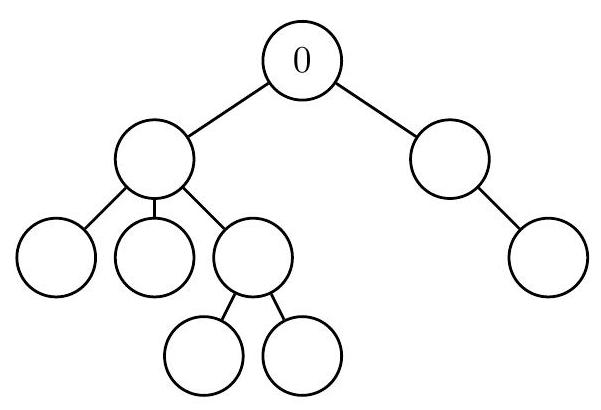
但不幸的是,你的珍贵进化树不小心洒上了咖啡。咖啡浸湿后,进化树的形状和最初生物(编号 $0$)还能辨认,但除最初生物外的其他生物的出生编号已无法识别。
你赶紧给每个生物临时编了个编号:最初生物的临时编号仍为 $0$,其余 $N-1$ 个生物被随机分配了 $1$ 到 $N-1$ 的不同编号。这些临时编号可能与出生编号相同,也可能不同,且不像出生编号那样保证父母生物的编号小于子生物。
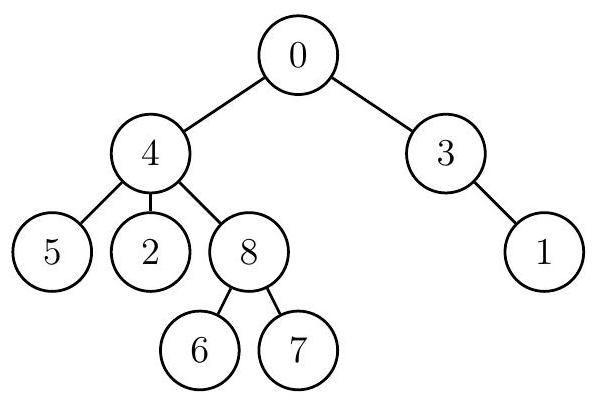
例如,同一进化树可能被临时编号如下图所示,每个节点标有临时编号。
幸运的是,你的电脑里存有进化树的备份,但备份文件被加密,你忘记了密码。好在备份程序还能用。程序提供了一个功能:输入两个生物的临时编号,它会告诉你哪个生物的出生编号更小。但若频繁使用这个功能,你的电脑可能会崩溃。因此,你需要编写代码,用尽量少的查询次数恢复进化树中所有生物的出生编号。
实现细节
你需要实现以下函数:
std::vector<int> recover(int N, std::vector<int> U, std::vector<int> V)- 该函数在一次执行中可能被调用多次。
U, V:长度为 $N-1$ 的整数数组。对于任意 $0 \leq i \leq N-2$,表示进化树中临时编号为 $U[i]$ 的生物是父母,临时编号为 $V[i]$ 的生物是子生物。所有 $V[i]$ 互不相同。- 你需要在每次调用中,通过调用后续定义的
compare函数(可调用 $0$ 次或多次),找出进化树中每个生物的出生编号,并将其存入一个大小为 $N$ 的std::vector返回。设返回值为 $X$,则对于所有 $0 \leq i \leq N-1$,临时编号为 $i$ 的生物的出生编号应为 $X[i]$。
程序可调用以下函数:
int compare(int a, int b)- $a$ 和 $b$ 必须满足 $0 \leq a, b \leq N-1$ 且 $a \neq b$。
- 若临时编号为 $a$ 的生物的出生编号小于临时编号为 $b$ 的生物的出生编号,返回 $1$;否则返回 $0$。
你提交的代码不得包含任何输入输出函数。
样例数据
假设 $N = 4$,$U = [0, 0, 0]$,$V = [1, 2, 3]$。评测程序调用:
recover(4, [0, 0, 0], [1, 2, 3])树的结构如下图:
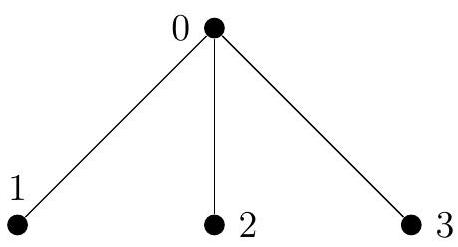
假设出生编号如下: - 临时编号 $0$:出生编号 $0$(固定) - 临时编号 $1$:出生编号 $2$ - 临时编号 $2$:出生编号 $3$ - 临时编号 $3$:出生编号 $1$
初始时,可能的出生编号排列有 $[0,1,2,3], [0,1,3,2], [0,2,1,3], [0,2,3,1], [0,3,1,2], [0,3,2,1]$,共 $P = 6$,故 $Z = \left\lceil \log_{2} 6 \right\rceil = 3$。
通过以下调用:
- compare(1, 2) 返回 $1$($2 < 3$)
- compare(2, 3) 返回 $0$($3 > 1$)
- compare(1, 3) 返回 $0$($2 > 1$)
- compare(0, 3) 返回 $1$($0 < 1$)
调用 $4$ 次后返回 $[0, 2, 3, 1]$,结果正确。此时 $C = 4$,$K = \frac{4}{3} \leq 1.4$,得满分。此样例满足子任务 $2$ 和 $4$ 的条件。
子任务
对于所有输入数据,满足:
- $2 \leq N \leq 10000$
- 对于所有 $0 \leq i \leq N-2$:
- $0 \leq U[i] \leq N-1$
- $1 \leq V[i] \leq N-1$
- $U[i] \neq V[i]$
- 输入数据构成一个有效的进化树。
- 一次执行中所有
recover调用中 $N$ 的总和不超过 $10000$。 - 本题的评测程序是非自适应的(NOT adaptive),即各生物的出生编号在程序开始时已固定,不会因
compare调用而改变。
详细子任务附加限制及分值如下表所示。
| 子任务 | 分值 | 附加限制 |
|---|---|---|
| $1$ | $1$ | 进化树中不存在与三个以上生物相邻的生物,且最初生物只与一个生物相邻 |
| $2$ | $7$ | 对于所有 $0 \leq i \leq N-2$,$U[i] = 0$ |
| $3$ | $12$ | 可为进化树中的每个生物重新分配一个颜色 $c$ $(0 \leq c \leq N-1)$,使得对于所有 $1 \leq i \leq N-1$,颜色为 $i$ 的生物的父母颜色为 $\left\lfloor\frac{i-1}{2}\right\rfloor$,且存在正整数 $k$ 满足 $N = 2^{k} - 1$。即进化树是完全二叉树 |
| $4$ | $80$ | 无附加限制 |
每次 recover 调用按以下方式评分。各子任务的得分取该子任务内所有测试用例中 recover 调用得分的最小值:
- 若程序异常终止或
recover返回值错误,得 $0$ 分。 在未知
compare提供的编号大小关系及子任务限制时,对于 $0 \leq i \leq N-1$,临时编号为 $i$ 的生物的出生编号为 $X[i]$ 的可能排列 $X$($0, 1, \cdots, N-1$ 的顺序)数量记为 $P$。因正确答案也是可能的 $X$ 之一,$P$ 为正整数。定义 $Z = \left\lceil \log_{2} P \right\rceil$,$C$ 为本次调用中compare的调用次数。得分由 $K = \frac{C}{Z}$ 决定。若 $Z = 0$ 导致 $K$ 未定义,则当 $C = 0$ 时 $K = 0$,当 $C > 0$ 时 $K = 2025$。若 $K > 20$,得 $0$ 分。
- 若 $8 < K \leq 20$,得该子任务分数的 $\left(5 \times \frac{20 - K}{12} + 5\right)$%。
- 若 $2.5 < K \leq 8$,得该子任务分数的 $\left(50 \times \frac{8 - K}{5.5} + 10\right)$%。
- 若 $1.5 < K \leq 2.5$,得该子任务分数的 $(20 \times (2.5 - K) + 60)$%。
- 若 $1.4 < K \leq 1.5$,得该子任务分数的 $\left(10 \times \frac{1.5 - K}{0.1} + 80\right)$%。
- 若 $K \leq 1.4$,得该子任务分数的 $100\%$。
样例交互库
示例评测程序接收测试用例数量 $T$,随后接收 $T$ 组输入,每组包括:
- 第 $1$ 行:$N$
- 第 $2$ 行:$PAR[1]\ PAR[2]\ \cdots\ PAR[N-1]$
- 第 $3$ 行:$Y[0]\ Y[1]\ \cdots\ Y[N-1]$
其中: - $PAR[i]$:出生编号为 $i$ 的生物的父母出生编号,满足 $0 \leq PAR[i] < i$。 - $Y[i]$:出生编号为 $i$ 的生物的临时编号,$Y[0] = 0$,且 $Y$ 是 $0, 1, \cdots, N-1$ 的排列。
对每个测试用例,程序根据进化树构造 $U$ 和 $V$,调用 recover,并输出:
- 若
compare(a, b)的 $a, b$ 不满足 $0 \leq a, b \leq N-1$,输出Wrong Answer [1]。 - 若 $a = b$,输出
Wrong Answer [2]。 - 若
recover返回数组长度不为 $N$,输出Wrong Answer [3]。 - 否则,第一行输出
C: 4($C$ 为compare调用次数),第二行输出recover返回值 $X$ 的元素。
输出 Wrong Answer 后程序立即终止。
注意,正确输出应满足 $Y[X[i]] = i$,但示例程序不验证这一点,且可能与实际评测程序不同。