题目描述
小 I 是一个巨大的铁路公司的主管,他管理着 $n$ 个火车站,用 $1$ 至 $n$ 的整数给它们编号。铁路公司有 $c$ 个分部,第 $i$ 个分部的办公室位于火车站 $p_i$。可能有火车站没有分部办公室,一个火车站也有可能有多个分部办公室。
$n$ 个火车站之间由 $m$ 条单向铁路连接,其中第 $i$ 条铁路由火车站 $u_i$ 连向 $v_i$,属于分部 $r_i$ 管辖。为了保证管理方便,分部 $r_i$ 的办公室要么在 $u_i$,要么在 $v_i$。
火车站 $1$(港口)和 $n$(首都)是公司管辖范围内最繁忙的车站。为了保障进口货物安全,根据交通运输部的要求,小 I 需要在一些铁路上设立检查站,使得从火车站 $1$ 到火车站 $n$ 的所有可能路线上都有一个有检查站的铁路。
小 I 可以通知一些分部(也可以不通知任何分部),要求这些分部在它们管理的所有铁路上设立检查站。小 I 想知道,最少需要通知多少个分部才可以达到要求。作为新上任的算法工程师,你准备给小 I 露一手。
输入格式
从标准输入读入数据。
输入的第一行三个整数 $n,m,c (2 \le n, m, c \le 5 \times 10^{4})$,分别表示火车站数量、铁路数量和分部数量。
接下来一行 $c$ 个整数 $p_1, p_2, \cdots, p_c (1 \le p_i \le n)$,描述每个分部所在的火车站编号。
接下来 $m$ 行每行三个整数 $u_i, v_i, r_i (1 \le u_i, v_i \le n, 1 \le r_i \le c)$,描述一条铁路。保证 $p_{r_i} = u_i$ 或 $p_{r_i} = v_i$。
输出格式
输出到标准输出。
输出一行一个整数表示最少需要通知的分部数量。
样例
输入
5 10 3
3 1 4
1 3 1
4 3 1
3 2 1
3 5 1
1 2 2
2 1 2
1 4 2
5 1 2
1 4 3
4 5 3输出
2解释
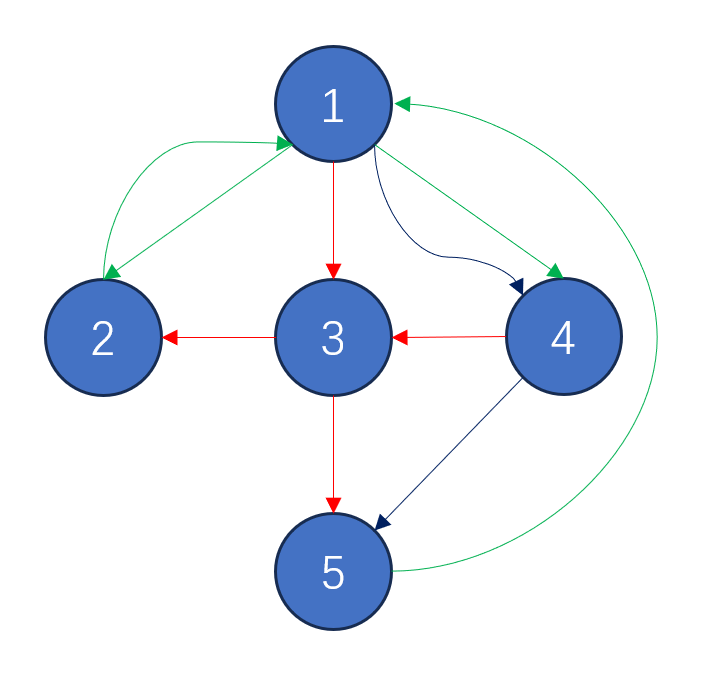
该样例的铁路组织如下图所示,其中红色、绿色和黑色分别为 1、2、3 分部管辖的铁路。最优策略是通知分部 1 和 3。