小 Q 是一名设计师，她主导着一个公园的设计。她已经设计好了每个景点的位置、内容，以及景点之间的路线。但是，对于如何设置景点周围的环境（主题），她就犯了难，因为对于有些道路，若两端的景点主题不一致，过渡会显得太突兀；对于另一些道路，若两端的景点一致，又会显得太单调；而且根据景点的内容，不同景点适合使用的主题也可能不同。她想通过一个程序来计算决定，哪些景点周围使用西部主题，哪些景点周围使用科幻主题，然而小 Q 的编程能力有限，所以她想让你帮忙解决这个问题。

公园有 $n$ 个景点，$m$ 条连接两个景点的无向道路。第 $i$ 条道路连接第 $x_i$ 和第 $y_i$ 个景点。
若第 $i$ 条道路两端的景点主题相同，可以得到 $c_i$ 的美观度；若第 $i$ 条道路两端的景点主题不同，可以得到 $d_i$ 的美观度。
第 $i$ 个景点使用西部主题可以得到 $w_i$ 的美观度，使用科幻主题可以得到 $s_i$ 的美观度。

公园的线路图是小 Q 精心设计的，小 Q 保证她设计的公园中从任意一个景点出发，能够到达所有的景点；保证每条道路连接的是两个不同的景点；保证没有两条不同的道路连接同一对景点；并且对于任意四个景点 $A,B,C,D$ ，使得其中任意两条路径除公共端点外没有公共点，且这六条路径分别连接四个景点中的每一对景点—— $AB,AC,AD,BC,BD,CD$ 。

以下给出一些一定不是小 Q 设计的公园线路图的例子：

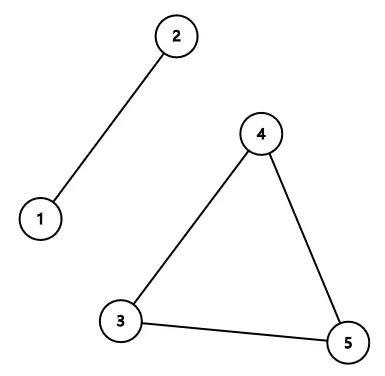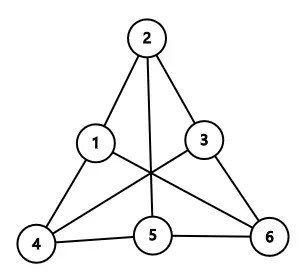从 $1$ 号节点出发不能到达 $3$ 号节点	对于第 $1,4,5,6$ 号景点，存在六条两两没有公共边的路径： $1\rightarrow4$，$4\rightarrow5$，$5\rightarrow6$，$6\rightarrow1$，$4\rightarrow3\rightarrow6$，$1\rightarrow2\rightarrow5$ 连接这四个景点的每一对景点

你需要把每个景点的主题设定为科幻主题和西部主题中的一种，使得所有景点以及道路的美观度之和最大。

小 Q 可能会通过重新计算来修改某个景点的 $w_i$ 和 $s_i$ 的值或者某条道路的 $c_i$ 和 $d_i$ 的值。她会修改 $Q$ 次，你需要在修改之前以及每一次修改之后输出最优方案的美观度之和。注意修改与修改之间不是互相独立的。

输入格式

第一行两个正整数 $n,m$ 。

接下来 $n$ 行，每行两个非负整数，其中第 $i$ 行表示 $w_i,s_i$ 。

接下来 $m$ 行，每行四个正整数，其中第 $i$ 行表示 $x_i,y_i,c_i,d_i$ 。

第 $n+m+2$ 行一个非负整数 $Q$ 。

接下来 $Q$ 行，每行三个正整数 $x,a,b$ ，若 $x \le n$ 则表示小Q把 $w_x$ 改为 $a$ ，把 $s_x$ 改为 $b$ ；若 $n < x \le n+m$ 则表示小Q把 $c_{x-n}$ 改为 $a$ ，把 $d_{x-n}$ 改为 $b$ 。

输出格式

输出 $Q+1$ 行，每行一个正整数，第 $1$ 行表示所有修改之前的答案，第 $i+1(1 \le i \le Q)$ 行表示第 $i$ 次修改之后的答案。

样例数据

样例输入

2 1
2 3
4 7
1 2 5 7
1
1 2 6

样例输出

16
18

样例解释

公园的线路图如图所示。

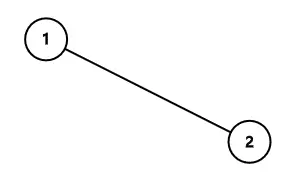
修改之前，最优方案为 $1$ 号景点使用西部主题，$2$ 号景点使用科幻主题，美观度之和为 $2+7+7=16$ 。

修改之后，最优方案为 $1$ 号景点使用科幻主题，$2$ 号景点使用科幻主题，美观度之和为 $6+7+5=18$ 。

样例输入

5 6
4 8
5 2
3 7
5 3
4 9
1 2 3 8
1 3 7 4
2 3 9 2
2 4 7 9
1 5 4 9
3 5 6 4
4
4 2 6
9 6 3
7 4 2
2 8 5

样例输出

72
71
70
68
71

子任务

保证 $2\le n \le 100000,Q \le 100000$；$x_i,y_i \le n$ ，$x \le n+m$ ，$s_i,w_i,c_i,d_i,a,b \le 10^6$。保证线路图是小Q设计的。

按照常理，公园是有出入口的。但是在本题中，你可以认为公园的出入口也是景点。

定义环路为起点和终点相同，并且中间（即除起点终点外）不经过重复景点的路径上道路的集合。

• 子任务 $1$（$2$ 分）：$Q=0$，$m=n-1$；
• 子任务 $2$（$3$ 分）：$n \le 17$，$Q\le 17$；
• 子任务 $3$（$7$ 分）：$Q=0$，每条道路最多属于一个环路；
• 子任务 $4$（$5$ 分）：$Q=0$；
• 子任务 $5$（$13$ 分）：$n,Q \le 1000$；
• 子任务 $6$（$19$ 分）：$s_i=w_i=0$，$x > n$，每条道路最多属于一个环路；
• 子任务 $7$（$17$ 分）：$s_i=w_i=0$，$x > n$；
• 子任务 $8$（$23$ 分）：$m=n-1$；
• 子任务 $9$（$11$ 分）：无特殊限制。