题目背景

题目背景与题目描述无关，可酌情跳过。

小 S 是一个喜欢音游的女孩子。

2077 年 7 月 7 日，某三维立体音乐游戏的 20.7.7 版本更新了一个塞满直角蛇的谱面 Tnemitnep [Beyond 18+]。但是当小 S 开始游玩这个谱面之后发现，由于游戏 bug，所有的蛇的色彩指示都没了……

但是小 S 作为 ptt 20.77 的 18 星高端玩家，首个理论值这首曲目的位置她势在必得，因此她不想等游戏开发者修复 bug。她决定：通过这个游戏的机制自行计算出所有蛇原本的颜色！

不幸的是，小 S 经过一些简单的推理，发现这个游戏的机制并不足以唯一确定所有蛇的颜色。因此小 S 首先希望通过这个游戏的“左蓝右红”规则计算出一种反手尽量少的染色可能性；同时计算出不同的染色方案数，以获知自己在最坏情况下需要尝试多少次才能正确地接住所有蛇。

小 S 将这个问题抽象成了一个 OI 问题，可是小 S 并不是很会 OI，于是她找到了即将参加 IOI 2024 的你。你能帮助小 S 在别人都还在莫名其妙红蛇 Track Lost 的时候拿下 Tnemitnep BYD 的首杀吗？

题目描述

在平面直角坐标系上给定 $ n $ 个矩形，形成若干个交点，每个矩形的所有边都平行于坐标轴。保证没有两个矩形的两条边共线。

矩形之间会形成若干个交点，每一个矩形都被它上面的交点分成若干段。定义属于一个矩形上的一段是该矩形上相邻的两个交点之间的部分。也就是说一个矩形上如果有 $ n $ 个交点，就会被划分成 $ n $ 段。

现在将每一个矩形上的每一段染色为蓝色或红色。要求：

• 与同一个交点相邻的同属于一个矩形的两段不同色；
• 所有红线形成若干互不相交的封闭曲线；
• 所有蓝线形成若干互不相交的封闭曲线。

定义两个图形 $ R,B $：

• $ R $ 为删去所有蓝线后，所有被奇数个红色封闭曲线包含的点组成的集合；
• $ B $ 为删去所有红线后，所有被奇数个蓝色封闭曲线包含的点组成的集合。

一个方案合法当且仅当它满足上述所有条件，并且使得 $ R\cap B $ 里面只有有限个点。

如果无法理解上述定义，可以参考样例解释。

你需要分别求出：

• 字典序最小的合法染色方案（字典序在输出格式里面有定义）。
• 合法染色方案数，对 $ 20051131 $（质数）取模。两个染色方案不同当且仅当存在一段，在一种方案中被染成红色，在另一种方案中被染成蓝色。

输入格式

第一行一个整数 $ n $。

接下来 $ n $ 行，第 $ i $ 行 4 个整数 $ x_{1,i},y_{1,i},x_{2,i},y_{2,i} $，前两个表示左下角坐标，后两个表示右上角坐标。

输出格式

第一行输出字典序最小的合法方案：如果无解，输出一行 -1；否则输出一个长度为 $ n $ 的 0/1 串。如果在你的方案中，按输入顺序给出的第 $ i $ 个矩形的左下角是红色，则你输出的第 $ i $ 个整数应该是 $ 0 $；否则应该是 $ 1 $。可以证明给定这些数之后能够唯一确定整个染色方案。如果有多解，你输出的解必须使得上面描述的 01 序列字典序最小。

第二行输出合法染色方案数，对 $ 20051131 $ 取模。无解时应输出 $ 0 $。

样例 #1

样例输入 #1

2
1 2 3 3
2 1 4 4

样例输出 #1

01
2

样例 #2

样例输入 #2

4
1 1 5 5
2 2 6 6
3 3 7 7
4 4 8 8

样例输出 #2

0000
2

样例 #3

样例输入 #3

2
1 1 4 4
2 2 3 3

样例输出 #3

00
2

样例 #4

样例输入 #4

3
1 2 4 5
2 3 5 6
3 1 6 4

样例输出 #4

-1
0

样例 #5

见下发文件中 $ \textbf{\textit{redandblue5.in}} $ 与 $ \textbf{\textit{redandblue5.ans}} $。

该样例满足子任务 3 的限制。

样例 #6

见下发文件中 $ \textbf{\textit{redandblue6.in}} $ 与 $ \textbf{\textit{redandblue6.ans}} $。

该样例满足子任务 4 的限制。

样例 #7

见下发文件中 $ \textbf{\textit{redandblue7.in}} $ 与 $ \textbf{\textit{redandblue7.ans}} $。

该样例满足子任务 5 的限制。

提示

样例 1 解释

如图是给定的矩形在平面直角坐标系上的形态。

如图，标出颜色的地方是属于第 1 个矩形的两段。

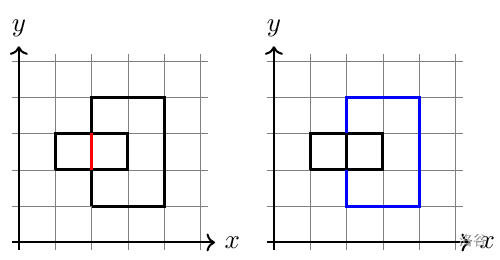
如图，标出颜色的地方是属于第 2 个矩形的两段。按照上述图片给出的颜色进行染色可以得到样例输出中给出的合法方案：

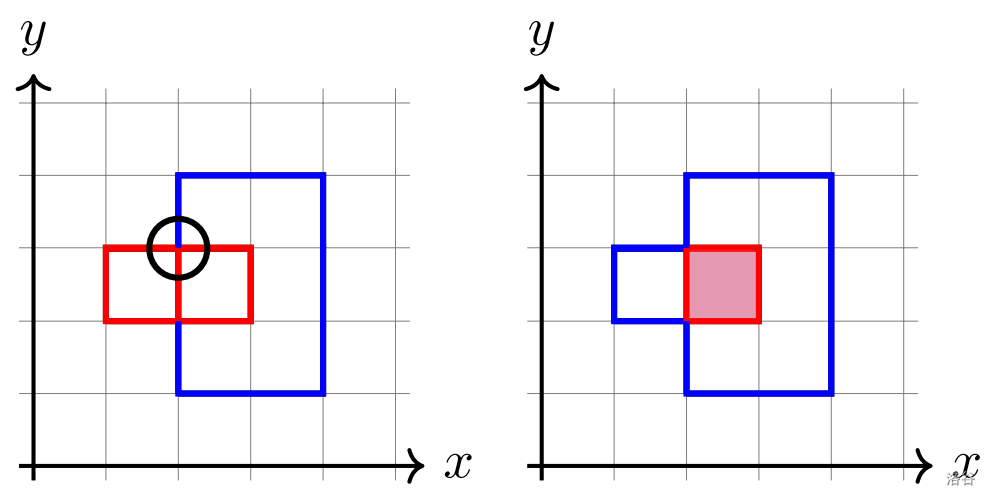
如下图，左侧方案是不合法的，因为与用圈标出的交点相邻的同属于一个矩形的两段同色；右侧方案也是不合法的，因为 $ R $ 与 $ B $ 交在图中的紫色正方形内，$ R\cap B $ 包含无限多个点。

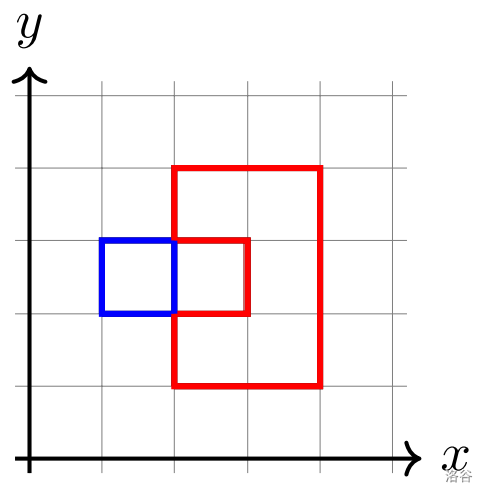
如下方案是合法的，但是对应字符串 10 不是字典序最小的。

样例 2 解释

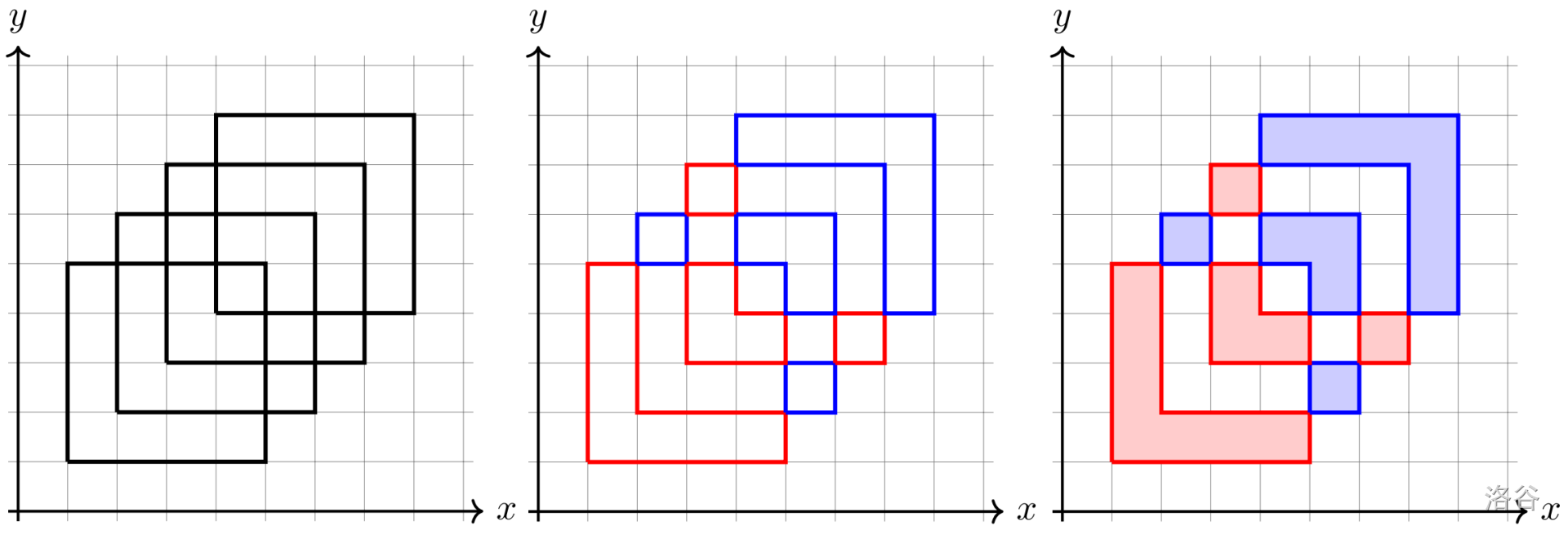
左侧的图为给定的所有矩形。

中间的图表示对应的染色方案。每一个矩形都包含 $ 6 $ 段，并且满足与任何一个交点相邻的同属于一个矩形的两段不同色。

右侧的图中，用红色区域标出 $ R $ 的范围，蓝色区域标出 $ B $ 的范围。两图形的交只包含 $ 12 $ 个点。

样例 3 解释

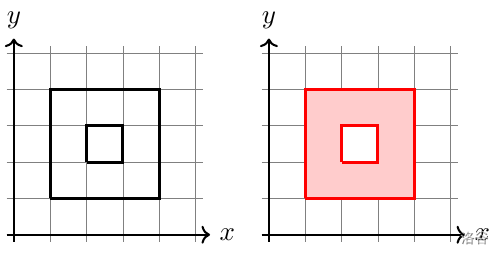
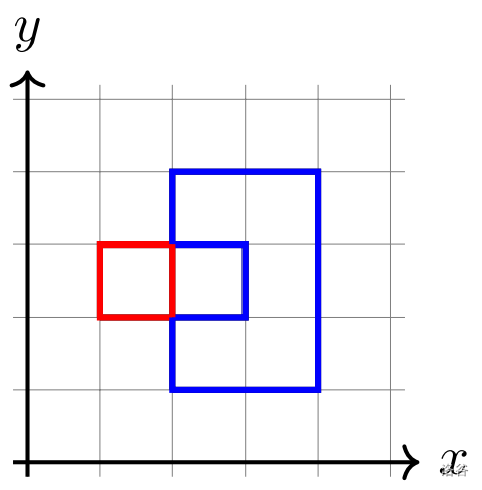
如图，该样例中，因为环内部的部分被 $ 2 $ 条红色封闭曲线包含，$ 2 $ 是偶数，所以环内部不属于 $ R $，$ R $ 形成一个环。

数据范围

对于 $ 100\% $ 的数据，保证 $ 1\leq n\leq 2\times 10^5 $，$ x_{1,i} < x_{2,i} $，$ y_{1,i} < y_{2,i} $，$ \{x_{i,j}|1\leq i\leq 2,1\leq j\leq n\}=\{y_{i,j}|1\leq i\leq 2,1\leq j\leq n\}=\{1,2,3,\cdots,2n\} $。