问题描述
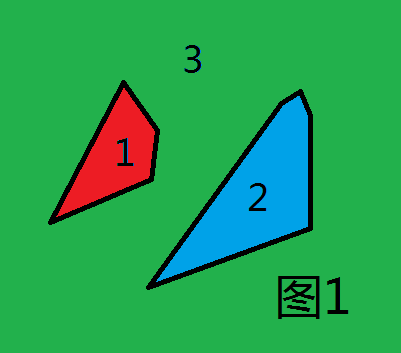
二维平面被划分成若干个简单多边形,每个简单多边形必与至少一个多边形共边,且多边形两两之间公共面积为0。所有多边形的并为一个简单多边形(即不存在图1所示情况)。
区域定义为:一个多边形,或者多边形的并关于平面的补集。
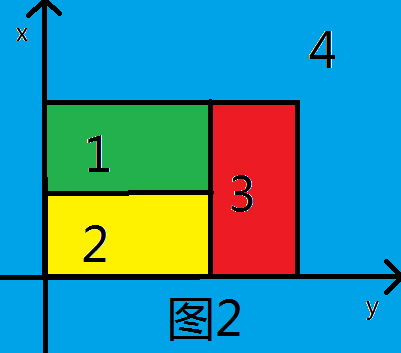
如图2,黑框表示三个简单多边形的边界,该平面共有4个区域。
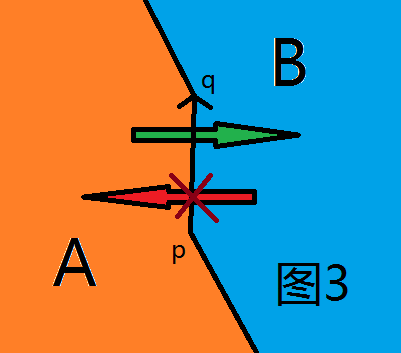
简单多边形的每条边 $⟨p, q⟩$ 有两个方向($p \to q$ 和 $q\to p$),每个方向有一个激活费用 $V$,表示激活这条边的该方向要花费代价 $V$。$V=0$ 则该边的该方向不可被激活。如图3,激活了该方向后,就能无数次从向量 $⟨p, q⟩$的逆时针方向走到顺时针方向,但不能从向量 $⟨p, q⟩$ 的顺时针方向走到逆时针方向,即从区域 $A$ 能走到区域 $B$,但不能从区域 $B$ 走到区域 $A$。
Wayne 希望你能帮他找到一个区域 $a$,使得任取一个区域 $b$,都能从 $a$ 出发到达 $b$。求在此区域 $a$ 下的最小总激活费用。保证存在这个区域。
输入格式
第一行两个整数 $n$ 和 $m$,表示点与线段的数目。
接下来 $n$ 行,每行两个整数 $x$ 和 $y$,表示第 $i$ 个点的坐标,点从 $1$ 到 $n$ 编号。
接下来 $m$ 行,每行四个整数 $p$,$q$,$V_1$ 和 $V_2$,表示存在一条从第 $p$ 个点连向第 $q$ 个点的线段,激活 $p \to q$ 这个方向的费用为 $V_1$,另一个方向费用为 $V_2$。
保证若两条线段相交,则交点是它们的公共端点。
输出格式
输出一行一个正整数,表示最小总激活费用。
样例输入
4 5
0 0
1 0
0 1
1 1
1 2 0 0
1 3 0 3
2 3 1 0
2 4 2 0
4 3 0 0样例输出
3样例说明
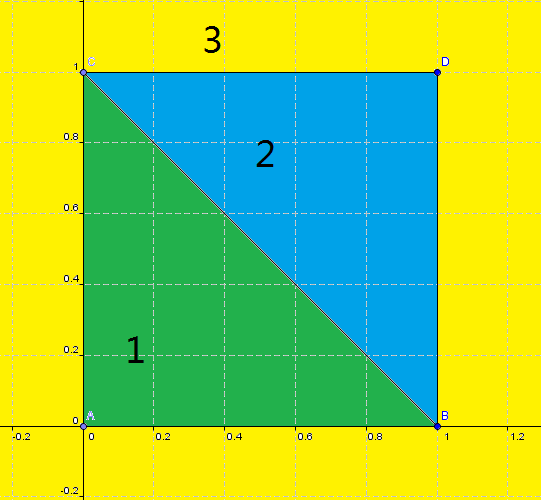
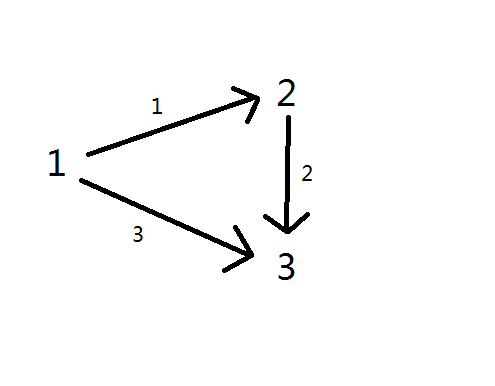
样例如左图,等价于右图所示有向图。则激活 $1 \to 2$ 与 $2\to 3$ 后,能从 $1$ 出发到达 $2$ 和 $3$。所以最小总激活费用为 $3$。
数据规模和约定
对于 $60\%$ 的数据,边的两个方向上激活费用相等;其中 $1/2$ 的数据,多边形由边长为 $1$ 的正方形组成,且所有多边形的并为矩形,如下图所示:

另外 $20\%$ 的数据,区域数 $\leq 18$;
另外 $10\%$ 的数据,区域数 $\leq 150$;
对于 $100\%$ 的数据,$n\leq 3\,000$,区域数不超过 $1\,000$,点坐标绝对值不超过 $10\,000$,每条边激活费用不超过 $100$。