题目描述
一年两度的THUPC又要来了,小C和小Z作为参赛无数届的老选手,自然也要来凑一番热闹。不过因为已经是老年人了,参赛自然是免谈了,但是他们对THUPC几年不换的logo产生了审美疲劳,为了更好地吸引大家报名,他们打算重画一个更花里胡哨的。
笑死,你怎么可能指望两个宅男码农有丝毫的艺术细菌?
他们深知这件事不在自己的能力范围之内,于是打算写一个人工智障来帮自己来画logo!
经过不懈的努力,他们的人工智障终于能跑起来了,不过他们很快就发现这个人工智障比自己还没有艺术细菌——它只会在平面上画水平和竖直的线段来拼成“THUPC”字样!
不过程序写都写了,不用白不用。小C和小Z针对程序的这一特性进行深入研究后制定了这样的规则:
对于每一条水平线段,设其横坐标区间为 $[l_i,r_i]$ ,纵坐标为 $y_i$; 对于每一条竖直线段,设其纵坐标区间为 $[d_i,u_i]$ ,横坐标为 $x_i$ 。上述所有数值均为整数,且满足$r_i > l_i,u_i > d_i$。
“THUPC”字样应当由 $15$ 条线段拼成,设其编号为 $1 \thicksim 15$ 。对于每一个字母,规则如下:
字母"T"由 $1$ 号水平线段和 $2$ 号竖直线段组成,满足 $d_2< y_1=u_2,l_1< x_2< r_1$ 。
字母"H"由 $3$ 号竖直线段、$4$ 号水平线段和 $5$ 号竖直线段组成,满足 $d_3=d_5< y_4< u_3=u_5,x_3=l_4< r_4=x_5$ 。
字母"U"由 $6$ 号竖直线段、$7$ 号水平线段和 $8$ 号竖直线段组成,满足 $d_6=d_8=y_7< u_6=u_8,x_6=l_7< r_7=x_8$ 。
字母"P"由 $9$ 号竖直线段、$10$ 号水平线段、$11$ 号水平线段和 $12$ 号竖直线段组成,满足 $d_9< y_{11}=d_{12}< u_9=y_{10}=u_{12},x_9=l_{10}=l_{11}< r_{10}=r_{11}=x_{12}$ 。
字母"C"由 $13$ 号竖直线段、$14$ 号水平线段和 $15$ 号水平线段组成,满足 $d_{13}=y_{15}< u_{13}=y_{14},x_{13}=l_{14}=l_{15}< r_{14}=r_{15}$ 。
生成的这 $5$ 个字母可以排布在平面的任何地方而无需从左到右排列,但是组成任意两个不同字母的任意两条线段不得相交。
需要注意的是,人工智障给出的线段顺序可能并不按照上述编号顺序;另外,给出的线段可能出现同方向线段的首尾相连、重叠或包含,此时应将其视为连续的一整条线段。
只有生成的线段在连接和排序后符合上述规范,才认为人工智障生成了一幅正确的logo;否则,如果出现多余的线段、缺少某条线段或坐标不满足要求等情况均为不正确的。
最后,小C和小Z要写一个程序来检验人工智障的每一份输出结果是否符合上述规范,不过熬夜连肝三天的他们终于累得爬不起来了,于是他们请你来帮忙。
输入格式
从标准输入读入数据。
第$1$行:一个正整数 $n$ 表示线段的个数,保证 $1 \leq n \leq 10^5$ 。
接下来 $n$ 行,每行先输入一个整数 $op_i$ ,必定为 $0$ 或 $1$ :如果 $op_i=0$ ,表示第 $i$ 条线段为水平线段,接下来输入 $3$ 个整数 $l_i,r_i,y_i$ 描述这条线段,保证 $l_i< r_i$ ;如果 $op_i=1$ ,表示第 $i$ 条线段为竖直线段,接下来输入 $3$ 个整数 $d_i,u_i,x_i$ 描述这条线段,保证 $d_i< u_i$ 。
保证输入的坐标均在 $[-10^9,10^9]$ 范围内。
输出格式
输出到标准输出。
如果符合规范,输出一个字符串 Yes,否则输出一个字符串No。
样例1输入
17
1 0 5 2
0 0 3 5
0 3 4 5
1 2 7 7
1 2 7 10
0 7 10 4
0 11 13 1
1 1 7 11
1 1 7 13
1 0 6 15
0 15 16 5
0 15 16 6
1 5 6 16
1 3 6 18
1 4 7 18
0 18 21 3
0 18 21 7样例1输出
Yes样例1解释
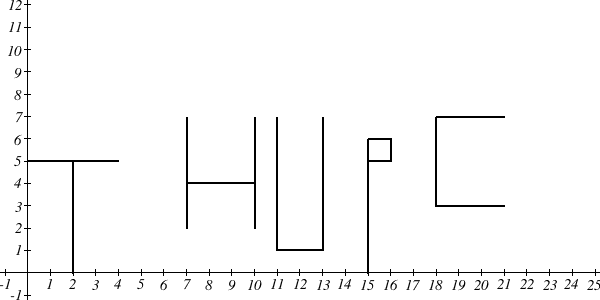
这组样例中,字母“T”的水平线段和“C”的竖直线段分别是由两条线段拼成的。