在电脑游戏《超级跳跃》中,英雄在一条山脊的各个顶点之间跳跃,目标是到达插有旗帜的终点位置,从而完成关卡。
游戏中的山脊由 $n$ 个依次排列的山峰组成,第 $i$ 个山峰位于位置 $i$,其高度为 $h_i$。对于任意 $i < j$,英雄可以沿直线从第 $i$ 个山峰跳到第 $j$ 个山峰,前提是飞行过程中直线上不会经过其他山峰。更正式地说,不存在这样的 $k$,使得 $i < k < j$ 且第 $k$ 个山峰的顶点(坐标为 $(k, h_k)$)严格位于连接点 $(i, h_i)$ 与 $(j, h_j)$ 的线段之上。
公司“战胜 AI”正在训练一个用于控制该游戏中英雄的神经网络。为了生成训练数据,需要回答若干个询问:对于一对下标 $l, r$($1 \le l \le r \le n$),求从编号为 $l$ 的山峰出发,英雄到达编号为 $r$ 的山峰所需的最少跳跃次数。
输入格式
第一行输入一个整数 $n$($1 \le n \le 10^5$)——山峰的数量。
第二行输入 $n$ 个整数 $h_1, h_2, \ldots, h_n$($0 \le h_i \le 10^{12}$)——各山峰的高度。
第三行输入一个整数 $q$($1 \le q \le 10^5$)——询问的数量。
接下来的 $q$ 行中,每行包含两个整数 $l_i, r_i$($1 \le l_i \le r_i \le n$)——对应一次询问的参数。
输出格式
对于每个询问,单独输出一行一个非负整数——所需的最少跳跃次数。
子任务
| 子任务 | 分值 | 附加限制 | 必要子任务 |
|---|---|---|---|
| 1 | 9 | $n, q \le 300$ | — |
| 2 | 9 | $n, q \le 5000$ | 1 |
| 3 | 14 | $h_i \le 10$ | — |
| 4 | 21 | 存在 $k$,使得对所有 $i$ 都有 $l_i \le k \le r_i$ | — |
| 5 | 27 | $n, q \le 5 \cdot 10^4$ | 1, 2 |
| 6 | 20 | — | 1–5 |
样例数据
标准输入
8 5 3 4 3 6 2 1 4 3 1 8 2 7 4 4
标准输出
2 2 0
说明
我们来分析样例中的第二个询问。英雄从第 2 个山峰到第 7 个山峰的路径可以如下所示:
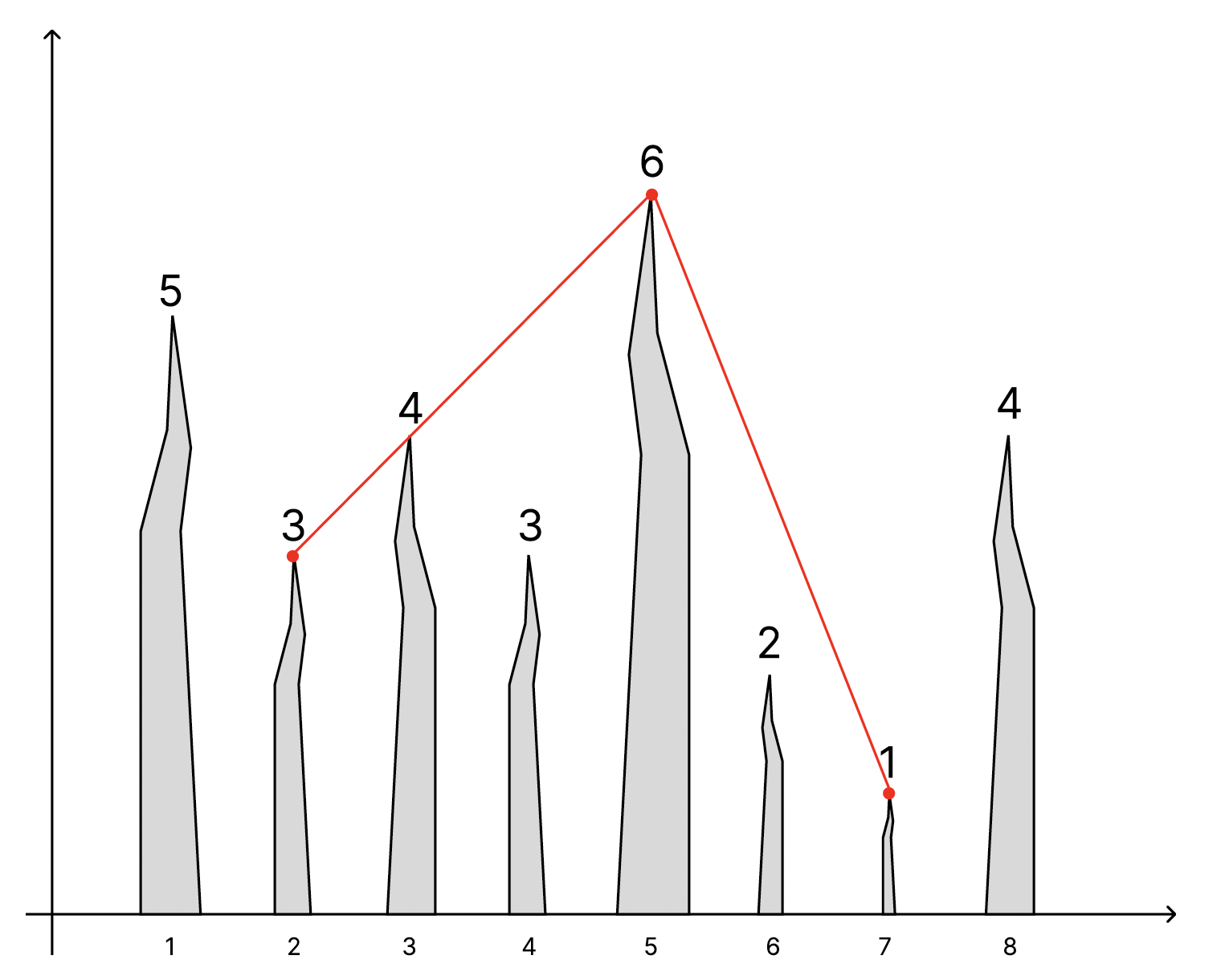
他将访问山峰 2、5 和 7,总共进行两次跳跃。