题目背景

我想要种一棵香蕉树 上面挂满我的所有祝福

题目描述

小 C 喜欢种树。

它种了一棵香蕉树，但是这棵树似乎需要人工维护才能生长。

因此，它经常会在树上的某一个位置挂上一些「祝福」。所谓「祝福」，其实就是一条链。

而有的时候树的一部分长得太好了，会导致整棵树长歪，所以它又不得不砍掉一部分。

小 C 还喜欢众数，所以它会经常问你所有树上结点的深度中同一个深度最多的出现次数。

具体来说，有一棵有根树，最初只有根结点 $1$，另外有一个变量 $n=1$。

有如下三种操作：

1. x l k：增加编号为 $n+1\sim n+lk$ 的结点以及边 $(x,n+1),(n+1,n+2),\dots,(n+l-1,n+l)$；$(x,n+l+1),(n+l+1,n+l+2),\dots,(n+2l-1,n+2l)$；$\dots$；$(x+n+(k-1)l+1),(n+(k-1)l+1,n+(k-1)l+2),\dots,(n+kl-1,n+kl)$。即在 $x$ 号结点下面挂了 $k$ 条长度为 $l$ 的链。这个操作执行之后 $n\gets n+kl$。
2. x：删除 $x$ 号结点及其子树。
3. （无参数）查询所有结点的深度中，出现最多的那个深度的出现次数。

输入格式

第一行包含一个整数 $m$，表示操作次数。

接下来 $m$ 行，每行包含若干个整数，第一个整数 $op$ 表示当前操作种类，接下来的输入与上面的格式依次对应。

输出格式

对于每个 $3$ 操作，输出一行一个整数表示答案。

样例 1 输入

23
3
1 1 2 3
3
1 6 2 2
3
1 7 1 4
3
2 12
3
2 13
3
1 3 1 2
3
2 7
3
2 3
3
1 5 2 3
3
2 6
3
2 5
3

样例 1 输出

1
3
5
6
5
5
6
4
3
5
3
2

样例 1 解释

下面的图中，点的颜色代表被加入的时间。

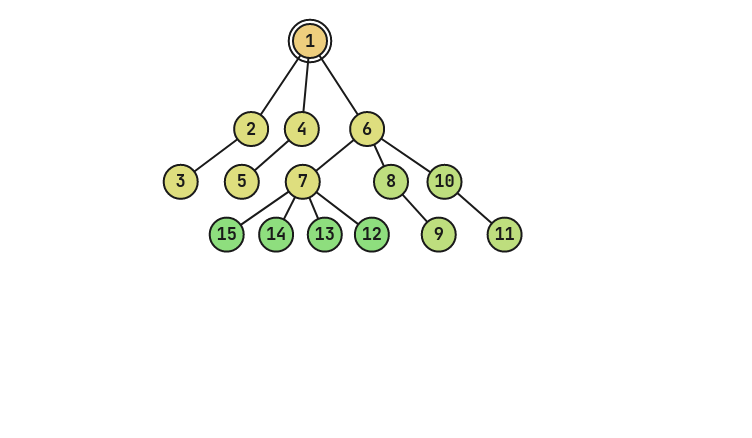
上图为经过三次 $1$ 操作（1 1 2 3，1 6 2 2 和 1 7 1 4）后的树。

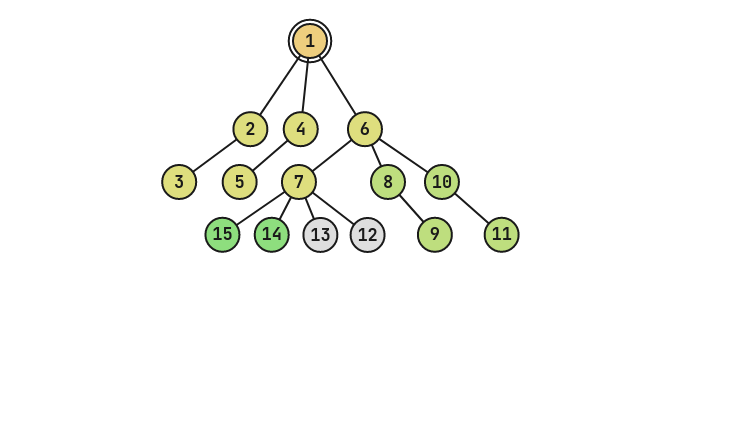
上图为在刚才的基础上经过两次 2 操作（2 12 和 2 13）的树。

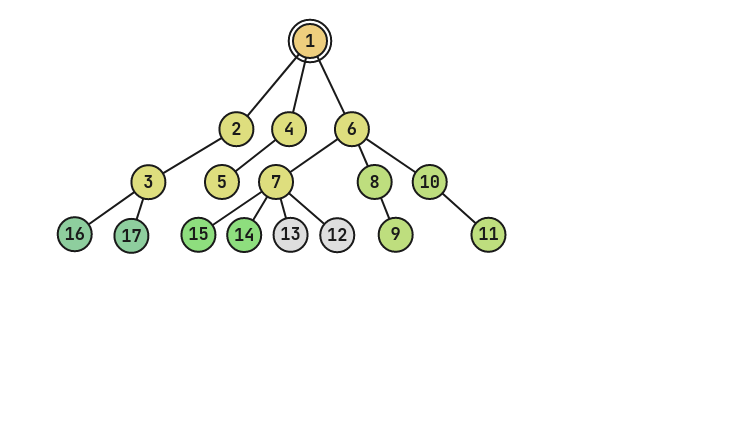
上图为刚才的基础上再经过一次 $1$ 操作（1 3 1 2）的树。

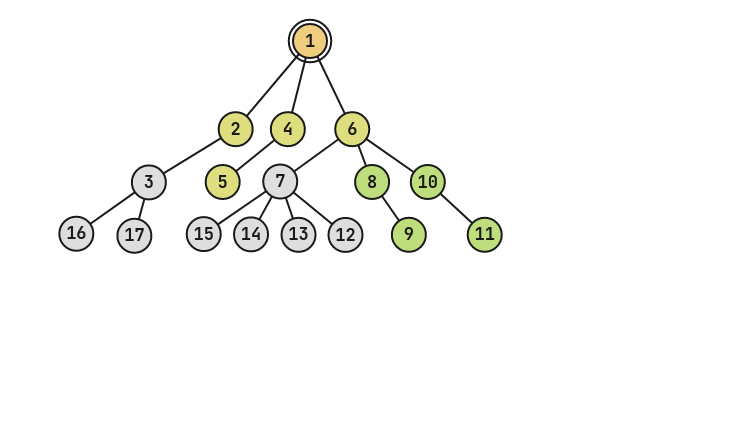
上图为刚才的基础上再经过两次 $2$ 操作（2 7 和 2 3）的树。

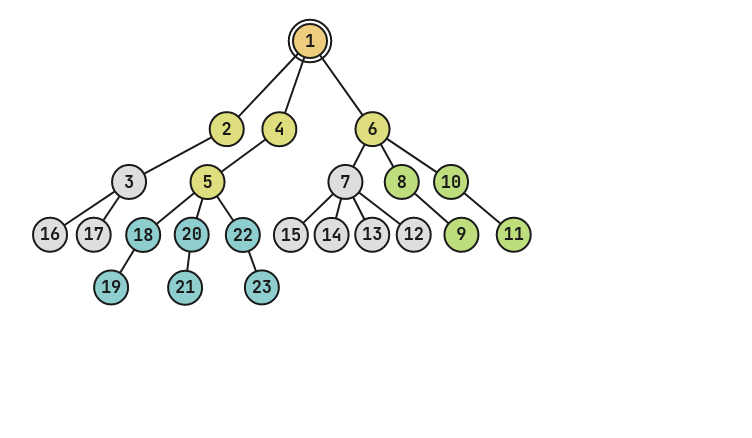
上图为刚才的基础上再经过一次 $1$ 操作（1 5 2 3）的树。

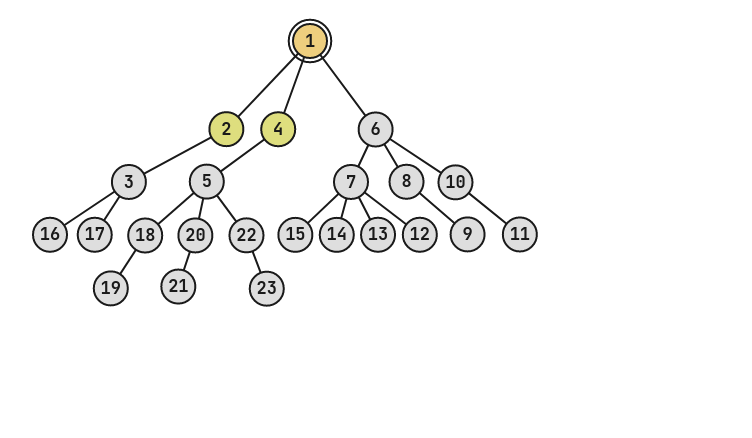
上图为经过所有操作后的树。

样例 2 输入

16
1 1 4 3
3
1 2 3 3
3
1 10 1000000000 2
3
1 1000000021 1 10
3
2 1000000027
3
2 23
3
1 12 1 1
3
1 2000000033 100000 1000000000
3

样例 2 输出

3
6
8
12
11
7
8
1000000001

样例 3 输入

18
1 1 85 483
1 32607 44 379
2 45784
1 46178 133 40
3
1 13506 152 357
2 62124
3
1 70877 209 33
3
1 37299 429 158
3
1 31487 258 363
2 159051
3
2 227162
2 279608
3

样例 3 输出

902
1257
1257
1415
1778
1778

样例 4 输入

19
1 1 189019619 113958
2 800361853
1 422490453 494478 254349561
3
2 1152812283
2 1650380207
3
1 4033287043 23425848 3533684
2 2666277906
1 709388173 159264263 191915
3
2 3453785850
2 8487830948768
2 39677822722745
2 167837684014594
1 1534084935 1205975 21949299
1 151207136 41249553 693236
1 1121564684 68403 1385595730
3

样例 4 输出

254463518
254463517
254463516
1386594833

数据范围

对于所有测试数据，保证：

• $1\le m\le 10^5$；
• $1$ 操作中的 $x$ 满足 $1\le x\le n$ 且 $x$ 号结点在树上依然存在，保证 $1 \le l,k \le 10^{18}$；
• $2$ 操作中的 $x$ 满足 $1< x\le n$ 且 $x$ 号结点在树上依然存在；
• 任意时刻的 $n$ 满足 $n\le 10^{18}$。

本题采用捆绑测试。

设操作过程中 $n$ 的最大值为 $k$。

• Subtask 1（10 points）：$k \le 5000$。
• Subtask 2（20 points）：$k \le 5 \times 10^5$。
• Subtask 3（20 points）：不存在 $2$ 操作。
• Subtask 4（20 points）：$1$ 操作中 $l$ 的值为 $1$。
• Subtask 5（30 points）：无特殊限制。