题目背景

题目名称意为：明年见。

小 R 是一个正在上高三的女孩子。她在升入高三的暑假复习了《种树郭橐（tuó）驼传》，便编出了这道与树有关的题。

在把这道题目丢给出题组后，她决定把全部时间和精力投入到高考的旅程中，期待在 2025 年的暑假在算法竞赛中与大家再会。

题目描述

请判断是否存在一棵树满足如下条件。若存在，请尝试给出构造。

树中包含 $n$ 个结点，编号为 $1\sim n$。另外，给定 $m$ 个点对 $(s_i,t_i)$，要求树上这 $m$ 条从点 $s_i$ 到点 $t_i$ 的路径覆盖每条边恰好一次 $^\dagger$。

若你正确判断了是否有解，但不会构造出这棵树，也可以获得一定的分数，详见【评分方式】。

$\dagger$ 称从点 $s$ 到点 $t$ 的路径覆盖一条边 $(u,v)$，当且仅当边 $(u,v)$ 在点 $s$ 到点 $t$ 的最短路径上。

输入格式

第一行包含两个整数 $n,m$，表示这棵树的点数和给出的点对数。

接下来 $m$ 行，每行两个整数 $s_i,t_i$，表示一个点对。

输出格式

第一行输出一个字符串 Yes 或 No（大小写不敏感），表示是否有解。

若有解，继续输出 $n-1$ 行，每行包含两个整数 $u_i,v_i$，描述一条边。你需要保证 $\boldsymbol{1\le u_i,v_i\le n}$ 且所有边构成一棵树。

样例 1 输入

6 2
1 2
3 4

样例 1 输出

Yes
1 5
2 5
3 5
4 6
5 6

样例 1 解释

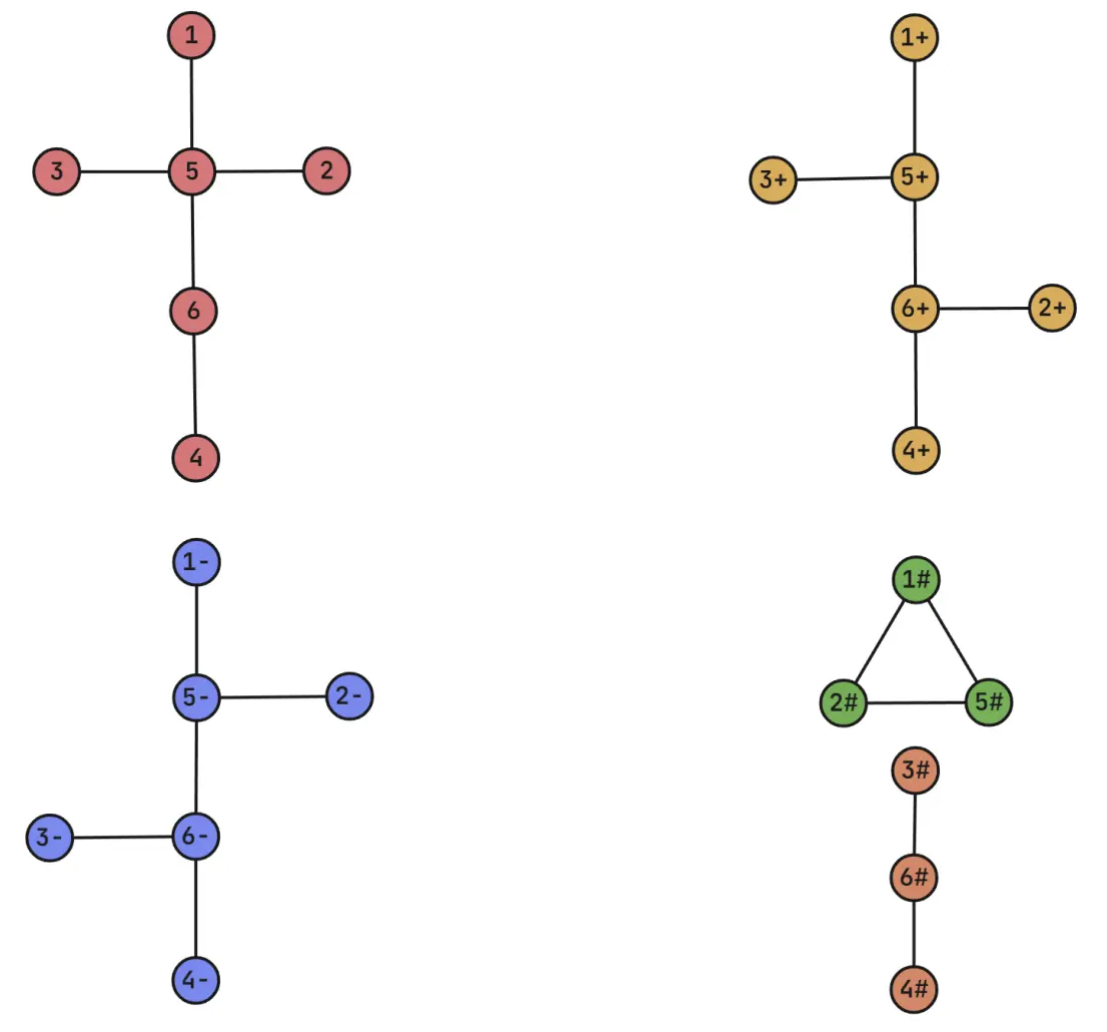
左上图为样例输出中给出的树。边 $(1,5),(5,2)$ 被路径 $(1,2)$ 覆盖，边 $(3,5),(5,6),(6,4)$ 被路径 $(3,4)$ 覆盖，符合题目要求。

右上图中边 $(5,6)$ 被路径 $(1,2)$ 和 $(3,4)$ 覆盖，不符合题目要求。

左下图中边 $(5,6)$ 未被任何路径覆盖，不符合题目要求。

右下图不是一棵树，不符合题目要求。

样例 2 输入

3 3
1 2
2 3
1 3

样例 2 输出

No

样例 2 解释

可以证明不存在符合要求的树。

评分方式

本题采用自定义校验器（Special Judge）进行评测。

对于每个测试点：

• 若第一行格式错误或与答案不匹配（大小写不敏感），得 $0\%$ 的分数。
• 若第一行答案正确且为 No，得 $100\%$ 的分数。
• 若第一行答案正确且为 Yes，但后 $n-1$ 行格式错误，得 $0\%$ 的分数。因此，请务必保证输出为一棵树。
• 若第一行答案正确且为 Yes，后 $n-1$ 行格式正确但树不符合要求，得 $20\%$ 的分数。
• 若第一行答案正确且为 Yes，后 $n-1$ 行格式正确且树符合要求，得 $100\%$ 的分数。

也就是说，对于第一个样例，在正确输出 Yes 的基础上，输出左上图可以得到满分，输出右上图、左下图可以得到 $20\%$ 的分数，输出右下图不能得到任何分数；对于第二个样例，正确输出 No 即可得到满分。

数据范围

对于所有测试数据，保证：

• $2\le n\le 3\times 10^5$；
• $1\le m\le 3\times 10^5$；
• $1\le s_i,t_i\le n$ 且 $s_i\ne t_i$。

本题采用捆绑测试。

• Subtask 1（10 points）：$n\le 3$，$m\le 3$。
• Subtask 2（10 points）：$n\le 10$，$m\le 10$。
• Subtask 3（20 points）：$m=1$。
• Subtask 4（10 points）：$n\le 300$，$m\le 300$。
• Subtask 5（10 points）：$n\le 2\times 10^3$，$m\le 2\times 10^3$。
• Subtask 6（20 points）：$m\le 2\times 10^3$。
• Subtask 7（20 points）：无特殊限制。