The rapidly growing popularity of Bytean chess is the reason why many different variants of this game have been invented. Because the traditional version is played on an infinite chessboard, what can be quite troublesome, sometimes simpler variants are chosen, in which the dimensions of the chessboards are bounded by 100 000 × 100 000. Some squares of the chessboard are black and the remaining ones are white, however the painting pattern depends on the particular chessboard. A pawn moves on such a chessboard in a bit different way than in traditional chess - it can move horizontally, vertically or diagonally to any of the adjacent eight squares provided that this square has the same colour as the square currently occupied by the pawn.

Examples of valid moves.

For given pairs of squares on the chessboard it should be determined whether a pawn can travel between these squares.

Input Format

The first line of the standard input contains three integers $ n $, $ m $ and $ p $ ($1 ≤ n ≤ 100\,000$, $1 ≤ m ≤ 1\,000\,000$, $1 ≤ p ≤ 1\,000$) separated by single spaces and representing the size of the chessboard, the number of black fragments of the chessboard described in the input, and the number of queries, respectively. The chessboard has dimensions $ n \times n $ and consists of squares with both coordinates between $1$ and $ n $. The following $ m $ lines contain descriptions of black fragments of the chessboard (they do not necessarily need to be disjoint). Each one of them consists of three integers $ w_{i} $, $ k_{i,1} $ and $ k_{i,2}$ ($1 ≤ w_{i} ≤ n $, $1 ≤ k_{i,1} ≤ k_{i,2} ≤ n $) separated by single spaces and meaning that in row $ w_{i} $ squares in columns between $ k_{i,1} $ and $ k_{i,2} $ are black. The squares that are not contained in any dark fragment specified in the input are white.

The following $ p $ lines contain the queries. Each query consists of two pairs of integers $ a_{i,1} $, $b_{i,1}$, $a_{i,2}$, $b_{i,2}$ ($1 ≤ a_{i,1}, b_{i,1}, a_{i,2}, b_{i,2} ≤ n $) separated by single spaces. The query is: can a pawn get from the square in row $ a_{i,1} $ and column $b_{i,1}$ to the square in row $a_{i,2}$ and column $b_{i,2}$?

Output Format

Your program should output $ p $ lines to the standard output: the answers to the respective queries, in the same order as they appear in the input. The answer to each query is a line with a word "TAK" (meaning YES) or "NIE" (meaning NO) without the quotes, depending on whether a pawn can get from the first of the specified squares to the second one without passing through a square with different colour.

Example

Input

4 5 2
1 1 1
2 3 4
3 2 2
4 2 2
4 2 2
1 1 3 2
1 2 4 4

Output

NIE
TAK

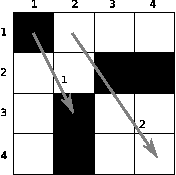
The chessboard and the queries from the example.