An undirected graph is called a cliquer if each connected component of the graph is a clique. Maurycy has drawn all cliquers with $ n $ vertices on a piece of paper and is going to assess beauty of each of them with a number from the set $\{1, \ldots, m\}$ (in particular, different cliquers may be assigned equal grades). In how many ways can he do this? The result should be computed modulo $10^{9} - 401$. The figure below depicts all cliquers for $n=3$.
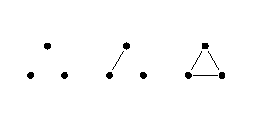
Input Format
The only line of the standard input contains two integers $ n $ and $ m $ ($1 \le n, m \le 200\,000$), separated by a single space and denoting the number of vertices of each cliquer and the number of grades respectively.
Output Format
The only line of the standard output should contain the number of possible sets of grades modulo $10^{9} - 401$.
Example
Input
3 2
Output
8