圆内任取三点其构成三角形覆盖圆心的概率
设三个点分别为 $P_1, P_2, P_3.$,圆上有 $x$ 个点 $.$ ($x$ 理论来说是无限大的,但是因为方便表述,所以使用 $x$ 代替之)
任选三个点,共有 $x^3$ 种方案。
概率为 $\dfrac{y}{x^3}$。其中 $y$ 表示圆内任取三点其构成三角形覆盖圆心的方案数。
作射线 $P_1 O$,$P_2 O.$ 两条射线与圆周的交点分别为 $Q_1,Q_2.$
显然,若确定 $P_1,P_2$ ,则满足题意的点 $P_3$ 一定在 $P_1 O$ 与 $\overset{\huge{\frown}}{Q_1 Q_2}$ 上。(原因不想写,让我写也可以试试看)
如图所示。
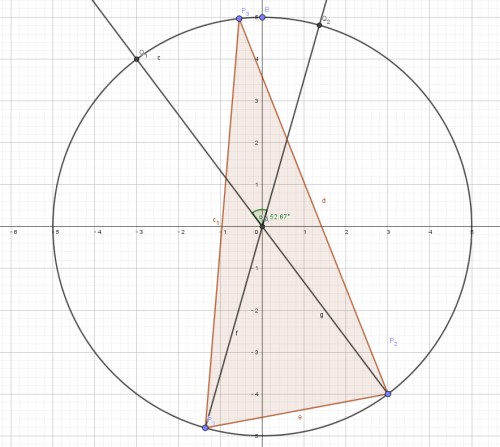
选择 $P_3$ 的方案数是 $2 \left[\dfrac{\alpha}{360} \times x \right] .$ 即 $2 \left[ \overset{\huge{\frown}}{Q_1 Q_2} \right].$ 对顶角相等,也即 $2 \left[\overset{\huge{\frown}}{P_1 P_2} \right].$
则总方案数为
$\begin{aligned} y & = 2\left[ \sum _{P_1=1} ^x \sum _{P_2=1} ^{\dfrac{x}{2}} \overset{\huge {\frown}}{P_1 P_2} \right]\\ & = 2\left[ \sum _{i=1} ^x \sum _{j=1} ^{\dfrac{x}{2}} j \right] \\ & = 2\left[ \sum _{i=1} ^x \sum _{j=1} ^{\dfrac{x}{2}} j \right] \\ & = 2\left\{ \sum _{i=1} ^x \left[ \dfrac{\frac{x}{2}(\frac{x}{2}+1)}{2} \right] \right\}\\ & = 2x \left[ \dfrac{\frac{x}{2}(\frac{x}{2}+1)}{2} \right] \end{aligned}$
这里认为 x 是无穷的,则 $y = \dfrac{x^3}{4}.$
代入 $\dfrac{y}{x^3}$ ,得到 概率为 $\dfrac{\dfrac{x^3}{4}}{x^3}=\frac{1}{4}.$