题目背景
傅里叶荣升巴黎市交通部长。新官上任三把火,傅里叶决定重构巴黎市的交通系统。
题目描述
巴黎市的地图可以看成一个无限大的二维平面。傅里叶在上面修建了 $ n $ 条传送带:第 $ i $ 条传送带修建于 $ x\in[p_{i-1},p_i),y\in\mathbb R $ 的区域中。对于 $ x<p_0 $ 或者 $ x\geq p_n $ 的部分,傅里叶没有修建传送带。
当一个人处于第 $ i $ 个传送带的区域内时,他会受传送带影响强制以 $ v_i $ 单位长度每秒的速度向 $ y $ 坐标增加的方向移动。$ v_i $ 可能为负,此时其 $ y $ 坐标会以相应的速度减小。
在位于未修建传送带的区域上时,$ y $ 坐标不会受到传送带的影响。
除了受传送带带动以外,这个人自己也可以移动。为了避免在速度不同的传送带间移动时出现跌倒事故,傅里叶委托麦克斯韦设计了脚底附有钢板的鞋子,并且在传送带上安装了强力磁铁。穿上这种鞋子后,你将只能 沿着与某条坐标轴平行,可能与坐标轴同向或反向 的方向,以不超过 $ V $ 单位长度每秒的速度移动。有了这种鞋子,在从一个传送带移动到另一个传送带时,先前的速度不会被继承,这个人将立刻按照新传送带的移动速度来移动。(自然,自身的移动还是可以同步进行的)
个人的运动与传送带的运动是叠加的。
在任意时刻,这个人都可以自由调整其运动的速率、方向;可以通过不断在极小间隔内切换方向以达到近似斜向移动的效果,甚至动态调整速率、方向达成近似曲线运动的效果;但是其任意时刻都只能有平行于坐标轴、不超过 $ V $ 的瞬时速率。
就算在没有铺设传送带的位置上,这个人仍然可以靠他的自由意志移动,不过还是只能沿坐标轴方向以不超过 $ V $ 单位长度每秒移动。(问就是麦克斯韦的靴子已经成为概念级装备了)
现在,傅里叶想知道他的交通系统究竟有多么伟大。因此,他向你提出了 $ q $ 组询问,每次询问如果有一个人要从 $ (x_1,y_1) $ 走到 $ (x_2,y_2) $,最少需要多少时间。因为傅里叶是唯一真神,所以他当然不会设计一个有缺陷的交通系统,因此所有的 $ v_i $ 均严格小于 $ V $,进而总是可以从一个位置走到另一处。(虽然这将会导致就算在最优情况下,通过传送带系统到达目的地的时间也无法小于原本的一半,更多的时候反倒更慢了,但是谁让他是交通部长,而你只是他手下的一个雇员呢?)
输入格式
第一行三个整数 $ n,q,V $,表示传送带数目、询问个数以及人的移动速度。
下一行 $ n+1 $ 个整数 $ p_0,p_1,\dots,p_n $,表示传送带的边界信息。
下一行 $ n $ 个整数 $ v_1,v_2,\dots,v_n $,表示每个传送带的速率。
接下来 $ q $ 行,每行四个整数 $ x_1,y_1,x_2,y_2 $,表示此次询问的起讫点。
输出格式
对于每次询问,输出一行一个实数,表示此次移动所需的最小时长,单位为秒。你需要保证输出与标准答案的相对或绝对误差不超过 $ 10^{-5} $。
- 如果你怀疑你的代码中出现了较大的精度误差,可以尝试使用更多整数和分数以规避浮点数运算,从而减少误差。
样例数据
样例 1 输入
1 2 10 -5 5 5 -10 -20 10 20 10 20 -10 -20
样例 1 输出
4.3333333333 6.5
样例 1 解释
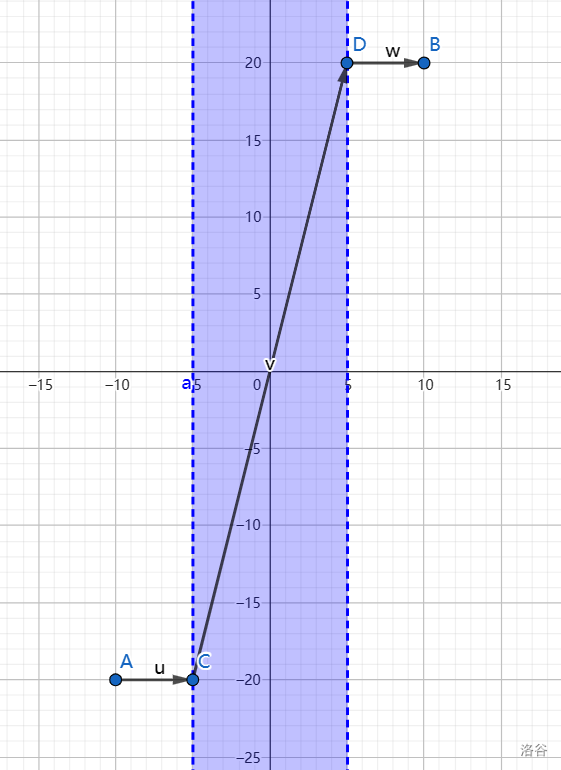
第一问中,上图是一种极优的行走方式。蓝色区域是传送带所在区域,在其上时我们以 $ (3,12) $ 每秒的速度移动(其中自身移动的速度是 $ (3,7) $,也即可以看作是三成时间沿着 $ x $ 轴正方向、七成时间沿着 $ y $ 轴正方向移动;在极短时间内不停切换,可以达成如上图中斜线行走的效果;$ (3,7) $ 的自身行走与 $ (0,5) $ 的传送带运转叠加成为 $ (3,12) $ 的速度向量)。
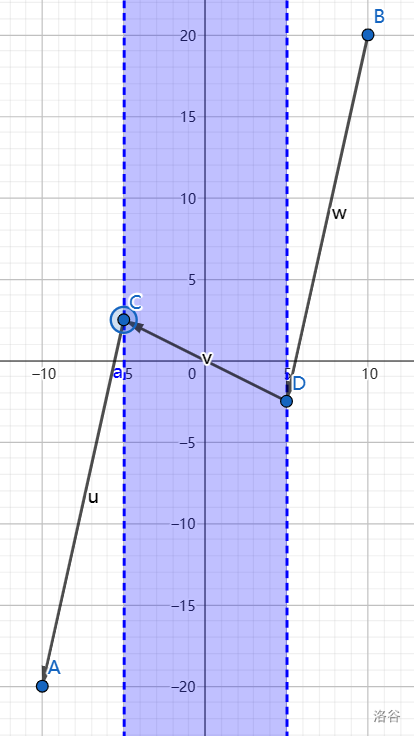
第二问中,上图是一种极优的行走方案。
需要注意的是,这两问中能达成最少时间的行走方案不止图中给出的两种。
样例 2 输入
1 4 10 -5 5 5 10 -10 10 10 10 10 10 -10 10 -50 10 50 10 50 10 -50
样例 2 输出
2 2 7.6666666667 10
样例 3 输入
5 5 10 -10 -5 0 5 10 15 9 -4 7 -6 2 -1 0 -9 -100 -7 0 7 10 9 0 -3 20 12 0 -17 -30 2 0 19 39
样例 3 输出
8.085714 1.815789 2.382353 4.987500 3.988235
样例 4~5
见下发数据。
数据范围
对于所有数据,均满足 $ n,q\leq1.5\times10^5 $,$ -5\times10^5\leq p_0<p_1<p_2<\dots<p_n\leq5\times10^5 $,$ |x_1|,|y_1|,|x_2|,|y_2|\leq5\times10^5 $,$ 0\leq|v_i|<V\leq5\times10^5 $。
Subtask 1(5%): 保证 $ n=0 $。
Subtask 2(10%): 保证 $ n,q\leq1000 $。
Subtask 3(10%): 保证对于所有询问,$ x_1=p_0,x_2=p_n $。
Subtask 4(10%): 保证所有询问的 $ x_1 $ 全都相等,所有询问的 $ x_2 $ 全都相等(但不保证 $ x_1=x_2 $)。
Subtask 5(15%): 保证 $ v_i $ 单调不降,且询问的 $ x_1\leq x_2 $。
Subtask 6(15%): 保证存在 $ i $ 使得 $ p_i=x_1=x_2 $。(但并不保证所有询问的 $ i $ 都相同)
Subtask 7(15%): 保证除 $ n,q,V $ 外,其它值都在合法范围内独立随机得到($ p $ 的随机方式是随机 $ n+1 $ 个不等的 $ [-5\times10^5,5\times10^5] $ 中的值并排序)。
Subtask 8(10%): 保证 $ n,q\leq5\times10^4 $。
Subtask 9(10%): 无特殊限制。