题目描述
在平面直角坐标系中,
给 $n$ 个点,这 $n$ 个点是可达的,如果点 $A,B$ 可达则线段 $AB$ 上的点均可达。
给 $m$ 个圆,问有哪些圆满足圆内任意点都是可达的。
输入格式
第一行一个整数 $T$,表示数据组数;
接下来 $T$ 组数据,每组数据中:
第一行一个整数 $n$,
接下来 $n$ 行每行两个整数 $x_i,y_i$,表示点,
接下来一行一个整数 $m$,
接下来 $m$ 行每行三个整数 $X_i,Y_i,R_i$,表示圆。
输出格式
每组数据输出一行,一个长度 $m$ 的 01 串,表示答案(0 表示圆内存在不可达的点,1 表示圆内所有点可达)
样例 #1
样例输入 #1
1 8 1 10 1 -10 10 1 8 -5 -10 0 8 6 -4 8 -6 8 15 2 -1 3 8 -1 6 -7 -10 2 -10 -1 4 7 10 10 -1 -7 9 -5 0 5 -5 5 4 10 -7 4 -5 5 1 2 1 6 10 3 7 -2 0 3 -2 0 7 -9 -6 6
样例输出 #1
100000000110100
提示
Idea:ccz181078,Solution:ccz181078,Code:ccz181078,Data:ccz181078
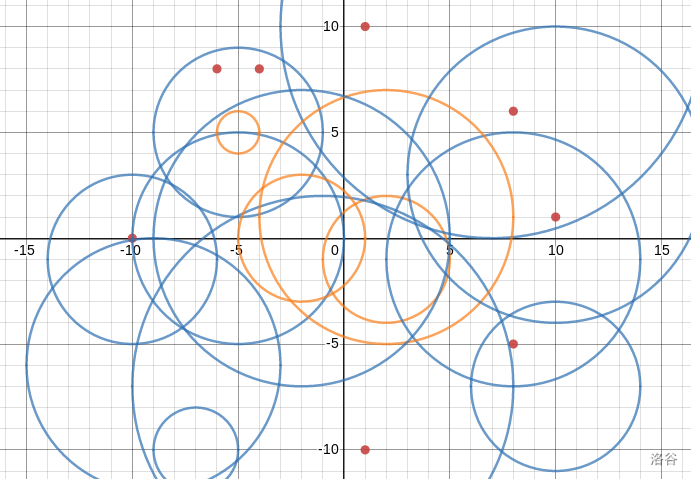
样例解释:
红色的点为样例中给出的点,橙色的圆表示答案为 1 的询问,蓝色的圆表示答案为 0 的询问。
$1\leq n,m\leq 5\times 10^5$,$1\leq R_i\leq 10^6$,$-10^6\leq x_i,y_i,X_i,Y_i\leq 10^6$,$\sum n\leq 5\times 10^5$,$\sum m\leq 5\times 10^5$。
保证当 $R_i$ 变化不超过 $1$ 时,答案不发生变化。