题目描述
access_globe 最近在玩一款城市规划的游戏。在游戏中,有 $n$ 个城市,$n-1$ 条可以双向通行的道路连接着这些城市,任意两个城市都可以通过这些道路互相到达。
最近,游戏中的“世界杯”比赛开始了。每一个城市都恰好支持一支球队,设第 $i$ 个城市支持的球队为 $a_i$。游戏给 access_globe 一个新的任务:选择一些城市,在这些城市建立可以承办世界杯的足球场。
access_globe 不希望建立足球场的城市所喜欢的球队的差异太大,因此他要求建立了足球场的这些城市中,不能存在 $3$ 个城市,使得它们支持的球队互不相同。同时为了减少球员花费在路上的时间,access_globe 希望任意两个建立了足球场的城市,都可以只经过其他建立了足球场的城市互相到达。
access_globe 是一个喜欢不同的同学,因此他希望你帮他求出,有多少种不同的建立足球场的方案。两种方案被认为是不同的,当且存在一个城市,使得该城市在恰好一种方案中被建立了足球场。
但你并不想帮他解决这个问题,你只想告诉他答案在 $998244353$ 进制下的个位(即答案除以 $998244353$ 的余数)。
输入格式
第 $1$ 行包含一个整数 $n$,表示城市的个数。
第 $2$ 行包含 $n$ 个用空格隔开的整数 $a_1,…,a_n$ ,表示每个城市支持的球队。
第 $3$ 到第 $n+1$ 行,每行包含 $2$ 个用空格隔开的整数 $x_i,y_i$ ,表示一条连接城市 $x_i$ 和城市 $y_i$ 的双向道路。保证任意两个城市都可以通过这些道路互相到达。
输出格式
输出一行一个数,表示不同的建立足球场的方案数除以 $998244353$ 的余数。
样例一
输入
6
5 1 1 3 2 6
1 2
2 3
3 4
3 5
2 6输出
15解释
城市的道路情况和支持的球队情况如下图,其中颜色相同的城市支持相同的球队
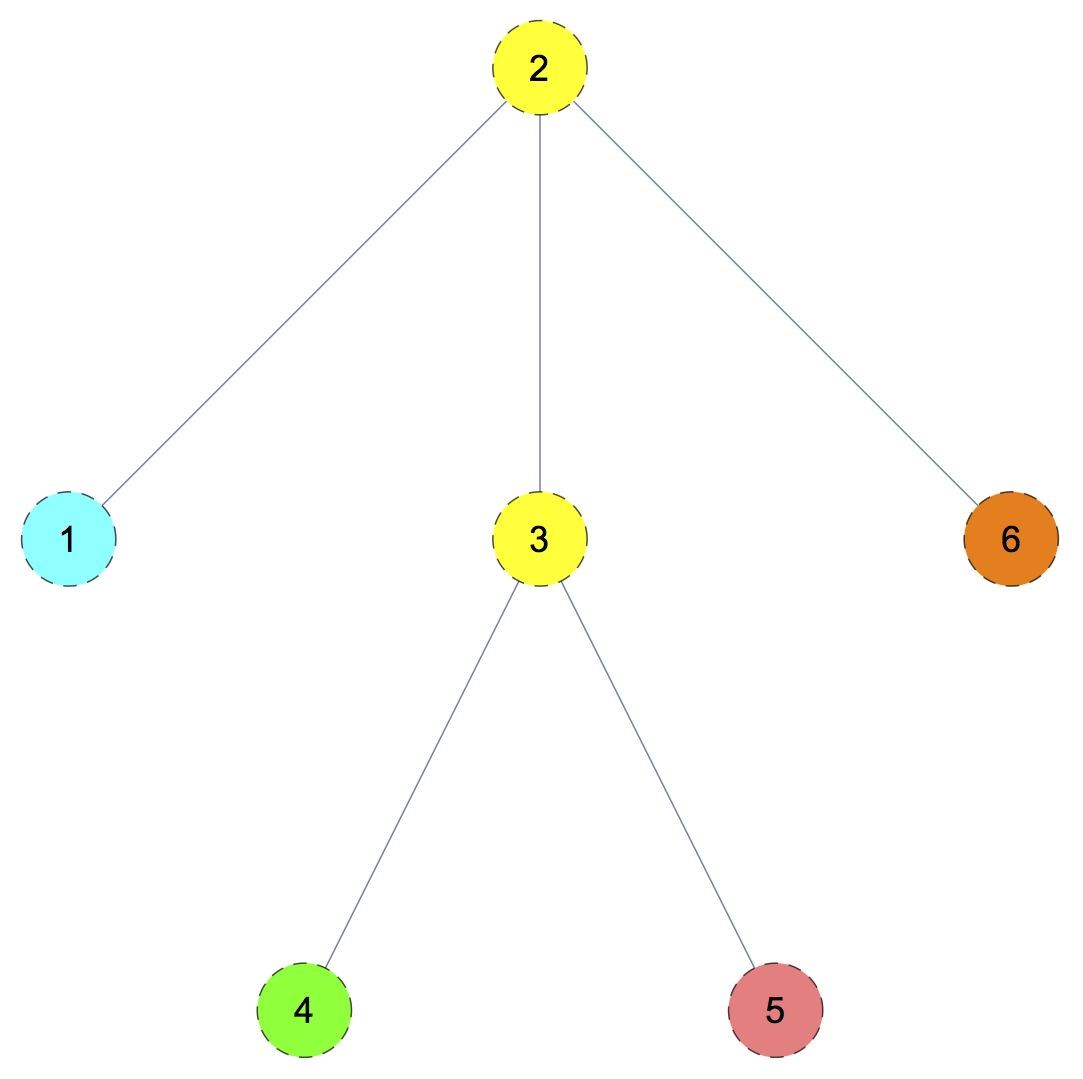
任何只建立一个足球场或将足球场建立在两个有道路直接相连的方案都是合法的,这样共有 $5+6=11$ 种方案。其余方案为在城市 $2$、$3$ 和其它任意一个城市建立足球场,共 $4$ 种方案,因此总共有 $15$ 种方案。
子任务
| 测试点 | 分值 | $n=$ | 特殊性质 |
|---|---|---|---|
| $1$ | $3$ | $500$ | 无 |
| $2$ | $7$ | $5,000$ | 无 |
| $3$ | $9$ | $2\times 10^5$ | A |
| $4$ | $13$ | $5\times 10^5$ | A |
| $5$ | $7$ | $2\times 10^5$ | B |
| $6$ | $11$ | $5\times 10^5$ | B |
| $7$ | $12$ | $5\times 10^4$ | 无 |
| $8$ | $14$ | $2\times 10^5$ | 无 |
| $9$ | $12$ | $5\times 10^5$ | 无 |
| $10$ | $12$ | $5\times 10^5$ | 无 |
对于所有数据,保证 $1\le a_i\le n\le 500000$。QOJ 中的 Hack 数据不受表格中等号限制。
在提交代码后将为你评测预测试数据并返回结果。本题的预测试数据包含 $10$ 个测试点,每个测试点的数据规模限制与对应编号的最终测试点相同。
注意:预测试数据的评测结果与最终评测结果没有关系。
提示
请注意本题的空间限制是 2 GB,请计算好程序的内存使用,不要超出限制。超出空间限制可能导致整道题目得 0 分。