Wojska króla Bajtomira podbiły właśnie kolejny skrawek terenu, jeszcze niedawno należący do królestwa Bitocji. Jednak aby móc chronić ten teren, należy wybudować warownię. Poddani króla są bardzo biegli we wznoszeniu dowolnie wielkich konstrukcji z kamienia i cegły, ale jedno, czego nie cierpią, to kopanie dołów. A jak wiadomo, każda warownia musi dla bezpieczeństwa zostać otoczona głęboką fosą.

Na szczęście na podbitym terenie znajduje się całkiem sporo strumieni, więc nadworny architekt Bajtazar postanowił wykorzystać je jako naturalną fosę. Zastanawia się teraz, gdzie postawić warownię, żeby z każdej strony otoczona była strumieniami. Bajtazar jest miłośnikiem symetrii, więc warownia musi zostać zbudowana na planie kwadratu. Ponieważ ma ona pomieścić oddział wojskowy oddelegowany do obrony podbitego terenu, musi być jak największa.

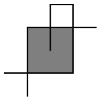
Królewscy geodeci nanieśli na prostokątną mapę położenie strumieni. Każdy z nich jest odcinkiem równoległym do jednej z krawędzi mapy. Odcinki reprezentujące różne strumienie mogą mieć więcej niż jeden punkt wspólny (tj. płynąć obok siebie w pomijalnej odległości). Warownię na mapie reprezentować będzie kwadrat. Musi on zostać tak umieszczony, żeby każdy punkt jego obwodu należał do pewnego odcinka reprezentującego strumień. Nie przeszkadza nam, jeśli odcinek reprezentujący strumień będzie przecinał wnętrze kwadratu (tzn. strumień będzie płynął pod warownią). Taki strumień można przecież zablokować kratą, a kucharzowi będzie łatwiej karmić pływające w fosie krokodyle.

Pomóż Bajtazarowi i odpowiedz na pytanie, czy da się zbudować warownię spełniającą powyższe wymagania. Jeśli tak, to wyznacz również maksymalną długość boku kwadratu reprezentującego warownię.

Input Format

W pierwszym wierszu wejścia znajduje się jedna liczba całkowita $n$ ($1 \le n \le 5,000$), oznaczająca liczbę odcinków reprezentujących strumienie na mapie. Kolejne $n$ wierszy zawiera opis poszczególnych odcinków - w $i$-tym z tych wierszy zapisane są cztery liczby całkowite $x_{1}$, $y_{1}$, $x_{2}$, $y_{2}$ ($-10^{9} \le x_{1},\ y_{1},\ x_{2},\ y_{2} \le 10^{9}$, $x_{1} = x_{2}$ albo $y_{1} = y_{2}$) oznaczające, że odcinek łączy punkty o współrzędnych ($x_{1},\ y_{1}$) i ($x_{2},\ y_{2}$).

Output Format

W jedynym wierszu wyjścia należy zapisać słowo NIE, jeśli nie da się zbudować warowni zgodnie z wymogami architekta. W przeciwnym wypadku należy wypisać jedną dodatnią liczbę całkowitą, oznaczającą największą długość boku kwadratu reprezentującego warownię.

Example

Input

6
-1 0 2 0
0 2 3 2
0 -1 0 2
2 0 2 3
1 1 1 3
2 3 1 3

Output

2